Zapageometría
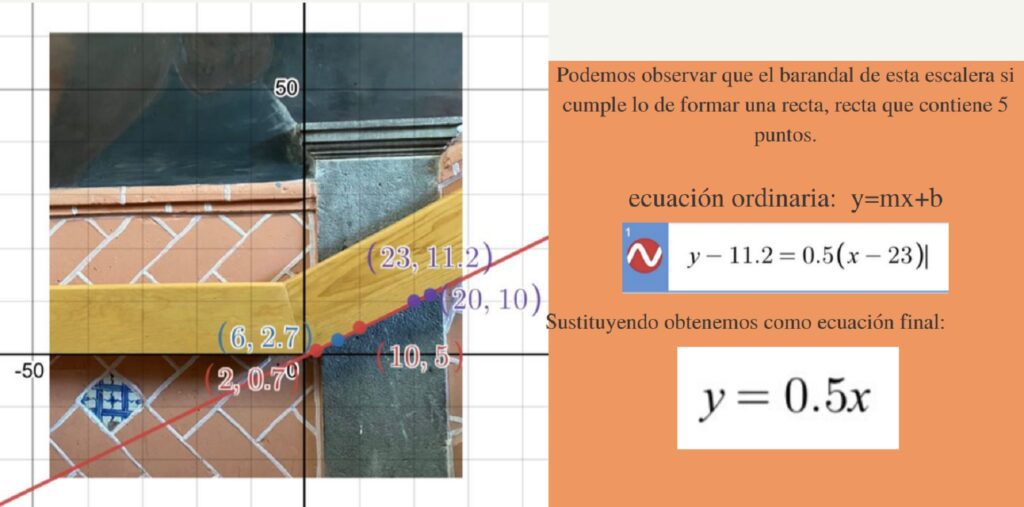
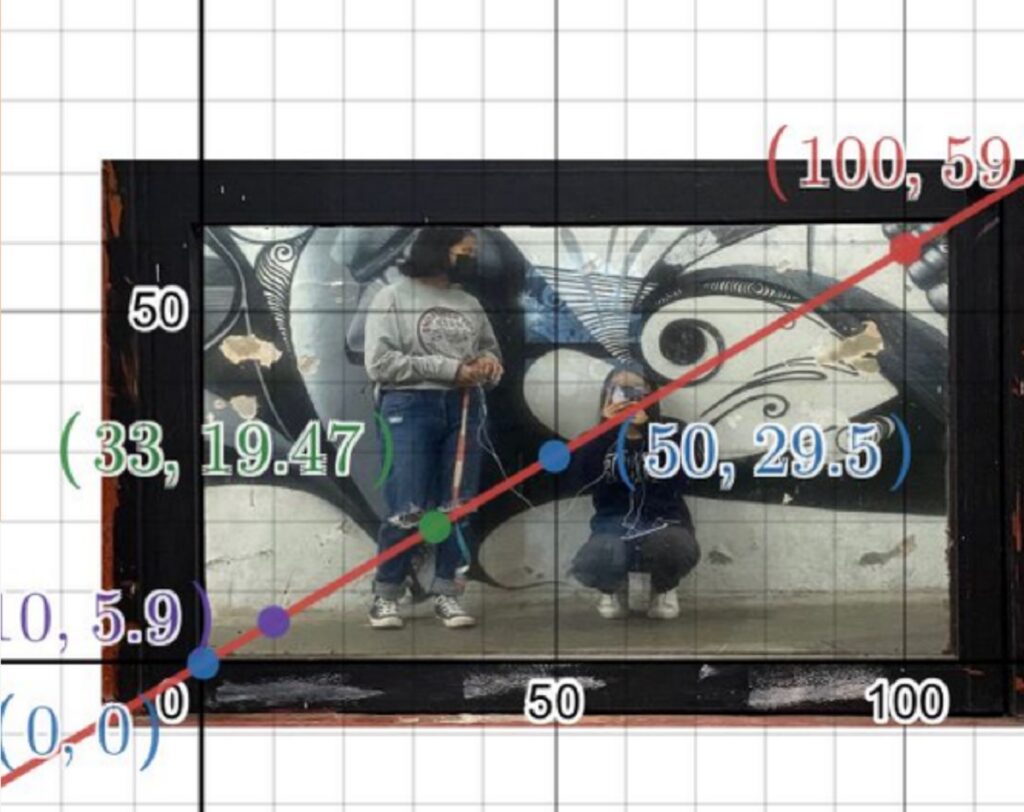
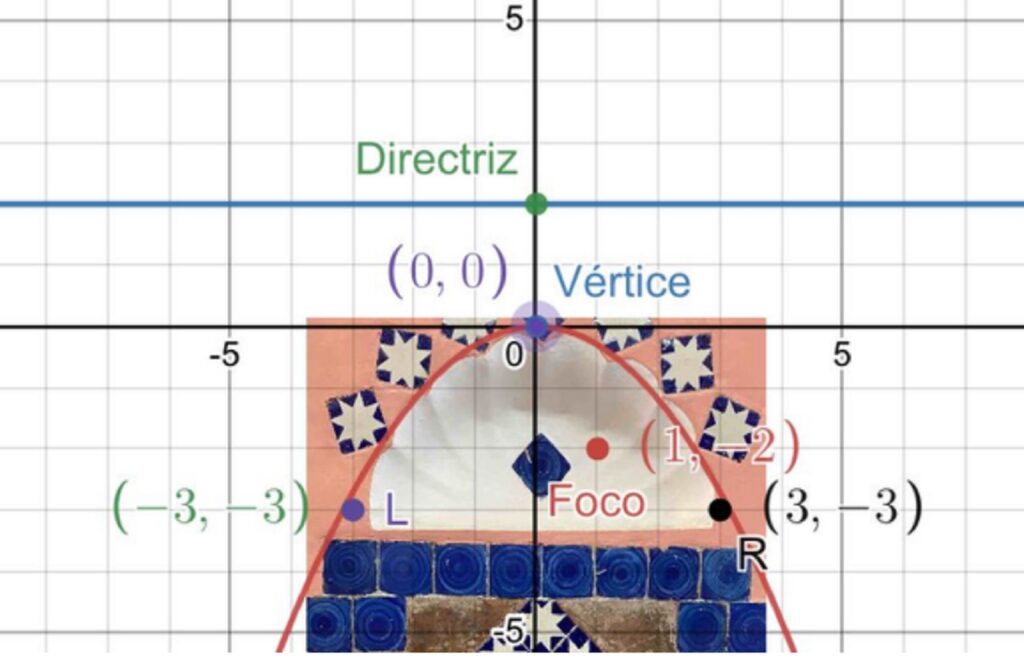
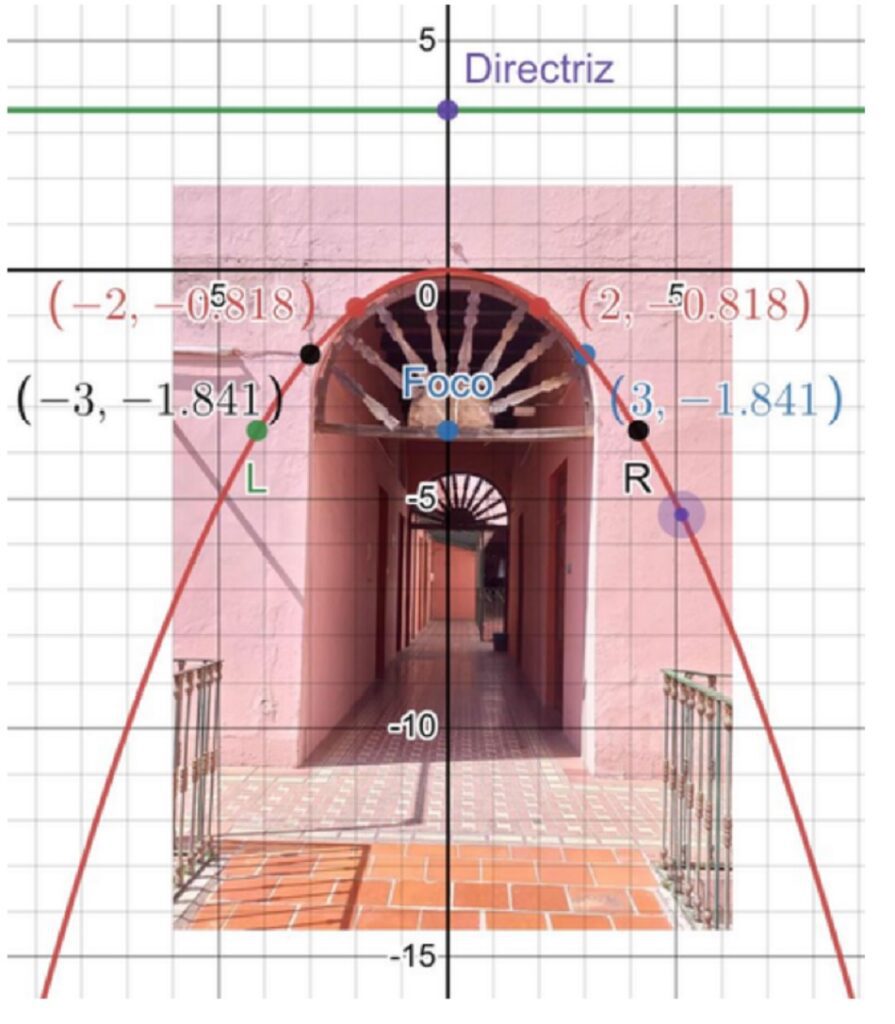
En la arquitectura de la preparatoria Emiliano Zapata de la BUAP, podemos apreciar distintas formas geométricas. Veremos cómo los temas de Geometría Analítica impartidos por el maestro Álvaro Cruz Ordóñez cobran sentido en las cosas que vemos día a día.